Создание Планеты - часть 1

А вы заметили, как в последние годы все чаще разработчики указывают на "процедурно-генерируемое нечто" как одну из ключевых особенностей той или иной игры? Генерируемые квесты, персонажи, подземелья, миры и даже галактики! Масштаб впечатляет. От квестов Скайрима, до подземелий Diablo 3 и звездных систем No Man's Sky формирующих галактику. Шанэй Нишри (Shanee Nishry), разработчик из Google разделяет это мнение и интерес к виртуальным мирам в играх. По этой причине она решила написать ряд материалов в которых рассказывает о том, как будучи программистом можно самому создать алгоритмы для генерации виртуальных миров. Ниже - перевод первого блога.

Возможно, это будет поучительно для молодых разработчиков игр. Учтите, я не программист графики, так что если что-то переведено неверно - пишите в ЛС, я исправлю. В комментариях не стоит этого делать.

Я всегда была фанатом процедурно-генерируемого контента; он позволяет создавать постоянно меняющиеся миры с потенциально бесконечным контентом. А еще это компенсирует мое отсутствие художественного таланта.

Процедурная генерация ландшафта полезна во многих играх. От скримиш режимов в стратегических играх, до подземелий в ролевых играх. В этот раз я исследую то, как генерировать планеты.

Работа с плоскостями и воксельной генерацией поверхностей позволили мне узнать множество алгоритмов визуализации, однако планеты на основе них создавать мне не приходилось. Надо это исправить.

План

Планеты в реальном мире содержат большое количество информации. Площадь поверхности Земли составляет что-то около 510 миллионов квадратных километров. Почти две третьих из них заняты водой и одна треть почвой. Это много данных, которые нужно создать.

Кроме того сушу пересекают реки, озера, различные типы биомов представляющих пустыню, джунгли, тундру и прочие. Информация о биоме может сказать вам о том, какие животные на территории обитают.

Также стоит вопрос освещения. Свет на Землю приходит от Солнца, которое можно представлять, как простой направленный источник света, однако необходимо учитывать тот факт, что свет рассеивается в атмосфере и частицы света под названием фотоны отталкиваются от частиц в Земной атмосфере и отражают больше голубого и желтого цвета. Это называется атмосферное рассеивание.

В этой главе я начну создавать базовую геометрию для основы планеты. В последующих материалах я добавлю больше деталей, включая карту высот, освещение, атмосферное рассеивание и прочие детали быстро повышающие требования к количеству данных на одну планету.

Геометрия

Первое что я сделала - это создала простую сферу используя простой алгоритм долготы и широты.

Однако проблема этого метода состоит в том, что на полярных шапках все полигоны сходятся в одной вершине, приводя к неравномерному распределению вершин, приводя к визуальным искажениям, особенно при накладывании текстур.

Поэтому я решила посмотреть на другие алгоритмы, интересными оказались Геодезическая и Кубическая проекции.

По первому впечатлению, геодезическая сетка ведет к отличным результатам, сохраняя сетку равномерной, без визуальных искажений, при этом показывая хорошую сферическую форму.

Геодезическая сетка может быть создана делением икосахедрона, добавляя новые треугольники и двигая их к радиусу сферы. Добавив тесселяцию можно получить гладкую сферическую форму с равномерной сеткой и без искажений.

Для простоты и скорости я решила использовать алгоритм кубической проекции. Используя формулу Филипа Ноуэлла найденную в сети я с легкостью могла спроецировать кубическую сетку на сферу всего в несколько строк кода:

// Для каждой вершины в меше
// Где вершины формируют шесть сеток создающих куб
// С границами от [-1, -1, -1] до [1, 1, 1]
void MapCubeToSphere( Vector3& vPosition )
{
    float x2 = vPosition.x * vPosition.x;
    float y2 = vPosition.y * vPosition.y;
    float z2 = vPosition.z * vPosition.z;

    vPosition.x = vPosition.x * sqrt( 1.0f - ( y2 * 0.5f ) - ( z2 * 0.5f ) + ( (y2 * z2) / 3.0f ) );
    vPosition.y = vPosition.y * sqrt( 1.0f - ( z2 * 0.5f ) - ( x2 * 0.5f ) + ( (z2 * x2) / 3.0f ) );
    vPosition.z = vPosition.z * sqrt( 1.0f - ( x2 * 0.5f ) - ( y2 * 0.5f ) + ( (x2 * y2) / 3.0f ) );
}

После создания сетки для каждой из сторон куба и используя код выше для каждой из вершин, куб схлопывается в сферу как показано на изображении ниже.

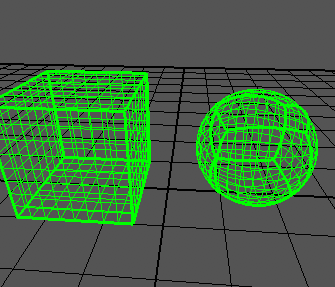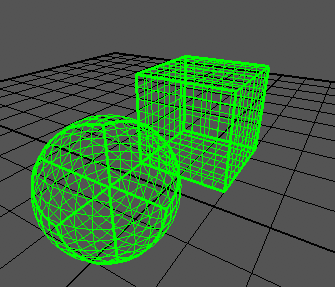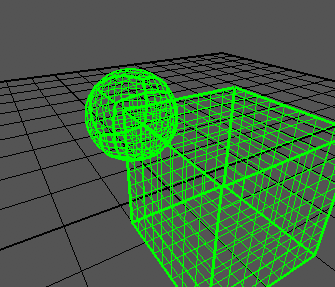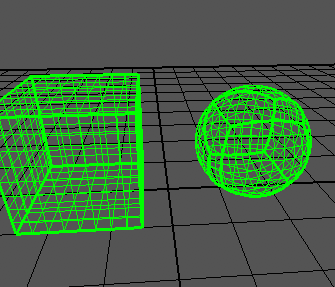
Код ниже показывает создание стороны куба и схлопывание в сферу:

// Переменные
// width             - количество вершин по оси X
// height           - количество вершин по оси Y
// radius           - радиус сферы
// pVertexBuffer - беффер массива вершин

// Сетка по направлению к негативной Z оси
Vector3 vMinPosition( -1.0f, -1.0f, -1.0f );

for ( int y = 0; y < height; ++y )
{
  for ( int x = 0; x < width; ++x )
  {
      Vector3 vPosition = vMinPosition;
      vPosition.x += (float)x / (float)(width-1) * 2.0f; // Умножить на 2.0f для переноса позиции с -1 на +1
      vPosition.y +- (float)y / (float)(height-1) * 2.0f; // Умножить на 2.0f для переноса позиции с -1 на +1

      // Проекция позиции сетки на позицию сферы
      MapCubeToSphere( vPosition );

      // Нормаль - всего лишь вектор из центра сферы.
      Vector3 vNormal = vPosition.Normal();

      // Экструдировать сферу по её радиусу
      vPosition *= radius;

      // Назначит в буффер вершин
      pVertexBuffer[ y * width + x ].Position = vPosition;
      pVertexBuffer[ y * width + x ].Normal = vNormal;
  }
}

Плюсы кубической проекции

У этого метода есть несколько преимуществ, которые я буду использовать

1. Сетка равномерная и схожа с ландшафтом создаваемым на плоскости, что делает работу с ним проще.
2. Работа с поверхностью как с сеткой позволяет визуализировать каждую сторону с разным количеством деталей используя такие алгоритмы как Chunked LOD и Geometry Clipmaps (разбиение полигонов для большей детализации).
3. Позволяет использовать кубическую проекцию для текстур, возможно, повышая производительность.

Больше о плюсах в следующих материалах.

Далее

В следующей части будут добавлены детали на нашу планету, которая на данный момент представляет собой простую сферу. В плоскостных сетках часто используется простое изменение Y-координаты для создания карты высот.

Карты высот требуют дополнительный работы прежде чем они могут быть наложены на сферу для того, чтобы переходы между разными сторонами схлопнутого куба были плавными.

В следующем материалу будут подробности генерации карты высот и способы повышения детализации.